The incumbent firm and all potential entrants have marginal cost=2 in an industry with inverse demand for a homogeneous product.

(1)Suppose that 2 new firms enter (at zero fixed cost) but that post-entry competition is described by the basic Cournot model. And the corresponding payoffs (profits)

(2)And suppose that there are entry barriers such that incumbents must sink a cost of K=25 in order to enter. In subgame perfect Nash equilibrium, how many firms will enter if post-entry competition is Bertrand? If it is Cournot

[ 解答 ]

(1) 題目說明市場內已有一家既存廠商，與兩家後進廠商 (2 、 3) ，所以 Stackelberg 與 Cournot 模型的混合，由既存廠商為領導者，而兩家後進廠商為追隨者，故以序列賽局的角度，應由後向前解

Stag1 先解 Followrs 決策，給定 Leader 已經決定產量Ｑ1 Followrs 極大利潤決策

第 2 廠商決策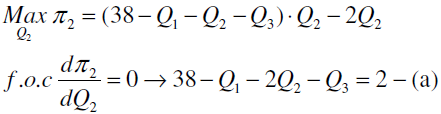

第 3 廠商決策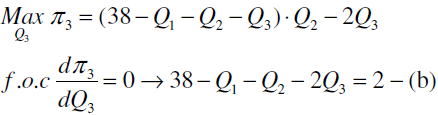

將 (a) 、 (b) 兩式聯立求解可得到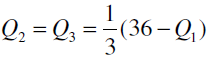代入 Leader 的目標函數

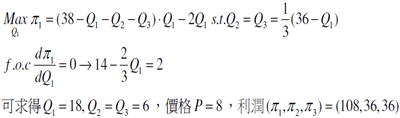
(2) 若後進者仍為 Bertrand 競爭，但有進入成本，而產品同質 ( ∵三家廠商面對相同的需求函數 ) 且邊際成本相同，由理論可知，價格競爭的結果 ，故既存廠商，但後進廠商必須付出 K=25 的進入成本，故，則選擇不進入市場，所以均衡廠商家數

之，若改為 Cournot 競爭，由第一小題可知，原本，但即使付出 K=25 的進入成本，新的利潤，仍有誘因進入市場，所以均衡廠商家數