各位同學大家好！又到了我們搞懂經濟大小事的時間，我們延續上一期的話題，就是航空公司服務品質低落與超賣機位的問題，上一次有說本期要用一個簡單的模型來說明航空公司的超賣決策，老實說這一段時間 張政 老師嘗試過很多模型，但是發現都太過於複雜不夠簡潔，到最後終於找到一個適合的簡單模型了，我們就直接來看看該怎麼設定。

其實很多新聞都有提到，航空公司之所以會超賣機位，其實就是賣出去的機位，旅客會同時搭乘的機會其實不高，簡單來說就是機率低於 100% ，其實這並不意外，可以想像現代人的行程通常很滿也很亂，臨時改變行程也不是什麼奇怪的事，特別是國內航線的機位，異動的情況可能就更多。我們假設如下：

(1) 航空公司原本賣的機位數量是 H ，為外生給定

(2) 超賣的機位數量是 q

(3) 航空公司面對的需求函數為 P(H+q) ，我們假設為簡單的線性函數 P=a-b(H+q)

(4) 旅客全部登記劃位的機率為 k ，相反的飛機上機位有空缺的機率就是 1-k

(5) 如果因為超賣機位和需要旅客下飛機的話，就要給補償金額 s ，雖然這些旅客日後還是需要服務他們，那我們也可以簡化，把未來的服務成本就加入這個 s 項之中。

(6) 飛機不論坐滿與否，都需要飛行的成本 TC ，我們可以把它視為一項固定的成本。

因此，航空公司面對的一個問題，就變成超賣機位的預期利潤的函數如下：

我們可以把這個函數合併為

故航空公司的決策為：

由一階條件（ F.O.C ）可以求出：

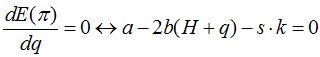
整理可得：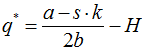

接著我們進行簡單的比較靜態分析

(1) 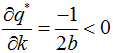，表示旅客全數到場的機率越高，那麼超賣的數量將會越低
(2) 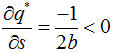，表示如果補償金額與日後的服務費越高， 那麼超賣的數量也會越低

上面的內容很符合我們的直覺，換句話說，只要旅客到場的機率「越低」，那麼航空公司就會大大的超賣機位；相同的，只要補償金額「越低」或者是不高，那麼航空公司就更有誘因去超賣機位，例如美國聯合航空的例子，他不需要持續的提高補償金讓旅客下飛機，只要找航警把旅客帶下飛機就可以了，但像美國聯合航空這一次就踢到了鐵板，後續的補償代價肯定是天價。

好的，這期的內容很簡單，其實就是透過模型，來分析超賣機位的決策與影響的因素，不過模型也可以變得更複雜一點，例如，將全數到場的機率改為內生決定的，也就是機率是超賣機位的函數，但這些都不會改變原始基本模型的結論， 各位同學也可以嘗試設計看看。

張政說經濟，我們下回見！！