[ 考題 105 政大經濟所 個體經濟學 第 3 題 ]

Assume that consumer、preferences are described by a Cobb-Douglas utility function in the following form, with two goods being consumed- apples ( ) and oranges

where the parameter α is the budget share for apples, and (1- α ) is the budget share for oranges.

(1) Derive the utility-maximizing demand functions for each commodity, for any expenditure level, Y, and for any prices of apples and oranges .

(2) Assume that apples and oranges each account for a fifty percent budget share, expenditure in the base period is one hundred, and the initial price of apples is four and of oranges is two. Calculate the utility maximizing quantities of applesand oranges.

(3)Assume that the economic shock has caused the apple prices to fall to two but that the orange price and total expenditure remain unchanged. Solve for the new, utility-maximizing quantities of apples and oranges.

(4) Calculate in monetary terms the impact on consumer welfare due to the

Above mentioned price change.

此題是非常基本的效用極大理論問題，同學只要掌握基本原則，即可完全解出，雖然是經濟研究所的考題，但也不會過於困難。

[ 解答 ]

個人效用函數為 Cobb-Douglas 形式： ，分別為蘋果與橘子兩種財貨，其中α為蘋果的支出份額

(1) 給定所得 Y ，商品價格為，求效用極大下的需求函數。

Step 1 ：最適消費條件為 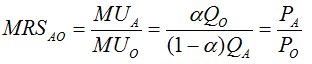，整理可得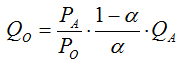

Step 2 ：代入預算限制式 ，整理可得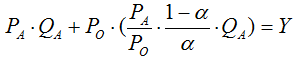 ，故蘋果的需求函數為 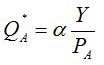、橘子的需求函數為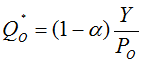

(4) 分別以補償變量與對等變量計算上述價格變動對消費者福利的影響

Step 1 ：給定，則可求得間接效用函數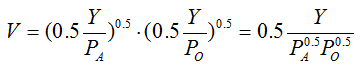，可計算價格變動前後的效用水準分別為

Step 2 ：間接效用的反函數即為支出函數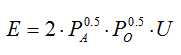：，故

補償變量
，而對等變量